Модель переноса радона
Решение проблемы прогнозирования пространственных масштабов ореола с повышенной концентрацией радона вокруг хвостохранилища (ХВХ) радиоактивных отходов в районе г. Кара-Балта требует проведения согласованных экспериментальных и расчетно-теоретических исследований. Само хранилище представляет собой в плоскости земной поверхности вытянутый прямоугольник размерами 2LX´2LY
~ 3006´1958м, в области которого имеет место повышенная по сравнению с природным фоном (в некоторых местах в 1000 раз) эксхаляция Rn, представляющая опасность для биологических организмов. Естественно, что наиболее опасен радон в приземном слое на высотах 1 –2 м над поверхностью, откуда он попадает в дыхательные пути человека.
Динамика распространения Rn в стороны от хранилища определяется пространственно-временными вариациями метеорологических факторов, таких как направление и сила ветра, скорость конвективного перемешивания воздушных слоев в приземном слое, количество осадков и т.д. В силу достаточно короткого времени жизни атомов этого химического элемента (период полураспада 3.8 дня) и малости коэффициента молекулярной диффузии в воздухе DM ~ 0.1см2/с, можно ожидать, что в тихую безветренную погоду радон практически не будет загрязнять атмосферу за пределами области над хранилищем. В этом случае будет происходить только вертикальный перенос радона за счет турбулентной диффузии, создаваемой конвективными потоками воздуха (рис.6).
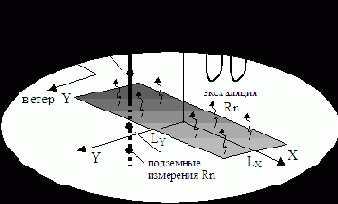
Рис.6. Схема распространения Rn в стороны от хранилища.
Постановка измерений концентрации Rn на разных высотах над площадью хранилища в тихие дни позволила бы определить величину коэффициента турбулентной диффузии DZ
в данном районе и его зависимость, в общем случае, от времени суток и удаления от земли z (из результатов многих исследований рассеивания примесей в атмосфере следует, что DZ ~ z). Анализ результатов таких измерений можно проводить с помощью подгонки решений одномерного стационарного уравнения диффузии:

где lRn=2.1×10-6с-1
– постоянная распада. Одно из граничных условий для этого уравнения очевидно: C=0 при z®¥. Второе граничное условие на поверхности земли получается из требования равенства эксхаляции радона из грунта потоку его атомов в атмосфере в точке z=0:

Здесь DG, CG – коэффициент диффузии и концентрация Rn в пустотном пространстве грунта, mG
– пористость грунта; характерный диапазон значений DG ~ 0.0005-0.05 см2/с. Известно, что стационарные распределения Rn вблизи земной поверхности неплохо описываются экспоненциальными законами:



Здесь KRn – коэффициент эманирования (выделения) Rn в пустотное пространство (поры, трещины), меняющийся для разных пород от сотых долей процента до ~ 50%; Q – темп наработки атомов Rn в единице объема подпочвенного слоя. Поскольку непосредственным источником этого химического элемента является a-распад радия, то величину Q принято представлять в виде:

и ARa – постоянная распада и атомный вес Ra.
Подставляя данные соотношения в граничное условие на земной поверхности, получим связь концентрации Rn в приземном слое C0 с величиной Q:

Эта связь дает возможность дополнительной оценки DZ путем измерения C0, если известен концентрационный состав урановых захоронений, а также величины KRn и m. Также необходимо знать коэффициент диффузии Rn в порах грунта DG, для чего можно провести дополнительные подземные измерения на 2-х – 3-х глубинах в пределах 1 м от поверхности.
Подводя итог, можно сказать, что систематические измерения при отсутствии ветра концентрации радона в Z-направлении совместно с численным моделированием позволяют оценить характерную высоту облака с его повышенным содержанием, подобрать коэффициенты модели, соответствующие изучаемому региону.
При этом надо иметь в виду, что из-за возможных случайных и систематических вариаций параметров эксхаляции - PRa , KRn, m результаты вертикальных измерений могут существенно отличаться в разных участках хранилища. Поэтому, желательно проводить достаточно большие серии таких измерений (десятки), чтобы набрать статистику.
После изучения стационарного радонового поля необходимо провести цикл моделирования ветрового переноса за пределы хранилища. Цель этого этапа моделирования состоит в определении теоретических пределов распространения вредной для здоровья концентрации Rn, а также нахождение метеорологических условий, наиболее способствующих такому распространению.
Для решения задачи ветрового переноса использовалось нестационарное уравнение миграции в существенно двумерной и даже трехмерной постановках:

где




В силу геометрических особенностей моделирование разумнее всего провести для двух направлений ветра: вдоль осей X и Y, ортогональных, соответственно, короткой и длинной сторонам хранилища. В первом случае общее уравнение миграции конкретизируется следующим образом:

а во втором:

Чтобы эти уравнения описывали реальные ситуации, необходимо подобрать коэффициенты поперечной диффузии DX, DY и задаться законами вертикальной стратификации скорости приземного ветра vвX(z) (либо vвY(z)). Для оценки коэффициентов диффузии, которые должны зависеть от силы ветра - DX(vвY), DY(vвX), разумнее всего провести в ветреные дни измерения концентрации Rn в приземном слое вдоль осей X,Y на различном удалении от хранилища, и затем, путем вариаций DX, DY , подогнать численные решения под полученные результаты.
Поскольку трудно организовать измерения, охватывающие временной период, в начале которого погода была тихой, а потом стала ветреной, то, скорее всего, речь может идти только о реализации измерений в условиях стационарного ветра в X- или Y- направлениях.
Соответственно, моделирование таких измерений должно проводиться в стационарной постановке с граничным условием в виде заданной в площади хранилища эксхаляцией радона. Что касается вертикального профиля скорости ветра, то известно, что в приземном слое выполняется закономерность:


Рассмотренная здесь модель применялась для решения следующих прогнозных задач:
1. В начальный момент (t=0) над хранилищем имеет место стационарное распределение Rn по высоте - C(z,t=0). В этот же момент включается ветер в X- или Y- направлении с заданной скоростью vвX(z), либо vвY(z). В ходе решения нестационарной проблемы переноса определялся темп спада максимальной концентрации Rn в приземном слое Сmax. В ходе счета достигался режим установления, когда Сmax(x,y,t) приближалась к фоновому значению. Исходя из расчетного темпа спада Сmax , можно оценить время исчезновения повышенной концентрации Rn при постоянном ветре.
2. Из общих соображений следует, что наиболее благоприятна для распространения Rn за пределы хранилища погода с периодическим нарастанием и затуханием ветра. В периоды затишья, после того как ветер унес очередное облако с повышенным содержанием Rn, эксхаляция из грунта приводит к возникновению над хранилищем нового подобного облака. Варьируя в расчетах длительности ветрового и спокойного периодов, можно спрогнозировать режим наиболее эффективного загрязнения окрестностей этим элементом, а также оценить предельные размеры области возможного загрязнения.