Численное исследование задачи
Полевые эксперименты показали, что между мощностью дозы g-излучения и содержанием Ra в подпочвенном слое хранилища наблюдается четкая линейная зависимость:

С использованием этой линейной зависимости можно определить источник радона в уравнении конвективно-диффузионного переноса в области грунта:



где rп – плотность породы, равная примерно ~ 2.5г/см3, ERn – коэффициент эманирования по радону; для вторичных (переработанных) пород, к каковым относится высохшая пульпа, содержащая радий, ERn
оценивается ~ 0.3 – 0.5.
Значения мощности дозы g
- излучения измерены по всей площади хвостохранилища и проинтерполированы на декартову сетку с размером ячейки DX = DY ~ 30м.
В результате уравнение конвективной диффузии записывается в виде:


Исходя из этого уравнения, сформулируем задачу на установление следующим образом:
1. Рассмотрим чисто диффузионный процесс -

2. Счетная область является параллелепипедом, характеризуемым координатами граничных точек Xmin=0, Xmax=1950м; Ymin=0, Ymax=3006м; Zmin= - 4м, Zmax= 4м.
3. Размер ячейки в плоскости XOY определяется дискретизацией g- фона и составляет 31´31м2. По оси Z количество точек, предположительно, должно быть ~ 20 в грунте и ~ 40 в воздухе; в силу принципиальной неоднородности распределения CRn в вертикальном направлении эти точки сгущаются вблизи границы грунт – воздух.
4. В начальный момент времени считаем, что во всей счетной области CRn(t=0,x,y,z)=0.
5. Граничные условия:
а) на границе z= Zmax величина CRn в каждый момент времени берется с предыдущего шага;
б) на нижней границе z= Zmin – ставится условие непроницаемости

в) на 4-х боковых границах в плоскости XOY – ставится также условие непроницаемости




6. Параметры уравнения: ux=uy=0, D=10-6м2/с, пористость m=0.2 .
7. Счет велся до установления стационарного решения; по диффузионным оценкам момент установления tкон ~ 106 – 107с.
В результате решения определялись следующие интегральные характеристики:
средняя концентрация по вертикали от поверхности земли до высоты h=4 м

средняя концентрация по всему пространству над хвостохранилищем до высоты h=4 м

коэффициент корреляции радонового поля и гамма-фона


дисперсия распределения радона по площади хранилища

На рис.16 представлено установившееся распределение CRn
на поверхности хранилища (z=0.5 см).
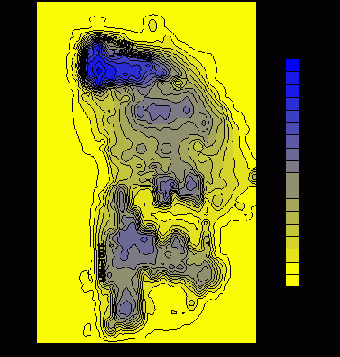
Рис.16. Распределение CRn (10-2 nKu/m3) на поверхности хранилища.
На рис.17 представлено установившееся распределение CRn
над поверхностью ХВХ (z=2м).
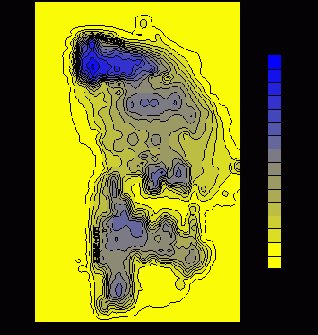
Рис.17. Распределение CRn (10-2nKu/m3) над поверхностью хранилища (z=2 м).
На рис.18 представлено распределение средней по высоте концентрации

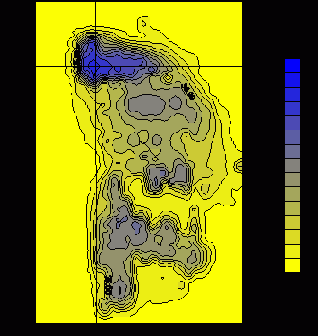
Рис.18. Распределение средней по высоте концентрации Cs(10-2nKu/m3).
На рис.19 представлено установившееся распределение CRn
над поверхностью ХВХ (z=0) в трехмерном виде, где в горизонтальной плоскости отложены координаты поверхности ХВХ, а по вертикали - значения концентрации.

Рис.19. Распределение CRn
(10-2nKu/m3) над поверхностью ХВХ.
При представлении результатов расчетов для дополнительной наглядности имеет смысл рассмотреть также одномерные распределения концентрации радона в некоторых характерных сечениях в продольном и поперечном направлениях. Подобные сечения, проходящие через область с максимальным уровнем g-фона и, соответственно, с максимальным значением CRn, изображены вертикальной и горизонтальной линиями на рис. 18. Продольное сечение в выбранной счетной области отвечает координате x0=594 м по оси OX, а поперечное сечение – координате y0=2398 м по оси OY. Графики одномерных распределений концентрации радона и g-фона в относительных единицах





Рис.20. Зависимости


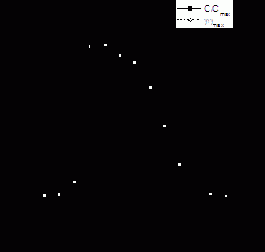
Рис.21. Зависимости


Данные зависимости демонстрируют, что пространственные изменения CRn практически совпадают с аналогичными изменениями g-фона, что является следствием относительно малого времени жизни атомов радона и медленного характера их диффузионного распространения в неподвижной атмосфере от места эксхаляции (за четверо суток они диффундируют на расстояния не более 20 метров). Результирующий коэффициент корреляции для безветренной погоды оказывается близок к единице: k ~ 0.9 (почти стопроцентная корреляция).
Полное расчетное установившееся количество радона в приземном слое над ХВХ составило C = 0.004 Ku, что соответствует средней концентрации C/h×S ~ 0.5 (nKu/m3). Дисперсия распределения радона по площади хранилища получилась сравнимой с этой величиной -
