Численное исследование одномерных
Приведем краткое описание постановки одномерных задач для расчета установившегося распределения концентрации Rn, выходящего из почвы в атмосферу.
Рассматриваются задачи о заполнении радоном первоначально пустого слоя, состоящего из 2-х однородных сред: от –z0 до z = 0 – грунт с пористостью m, от 0 до z1 – воздух (рис.7).
| ||||
| Рис.7. Геометрия задачи. |
При описании распределения радона в средах используется одномерное конвективно-диффузионное уравнение:

Основные параметры задачи:
коэффициент диффузии радона в грунте D1=0.05 см2/с,
коэффициент диффузии радона в воздухе D2=0.1 см2/с,
постоянная полураспада радона l=2.1×10-6 с-1,
пористость грунта m=0.2,
размеры рассматриваемой области z0=9м, z1=3м.
Здесь индекс 1 относится к грунту, а индекс 2 – к воздуху.
Данная задача рассматривалась в нескольких постановках:
· моделировался выход радона из грунта в атмосферу только за счет диффузии, когда в грунте действовал внутренний источник радона Q=lC0, равномерно распределенный по всей глубине (вариант 1);
· моделировался выход радона как в варианте 1, когда на глубине от 0 до 1 м не выделялся радон (вариант 2 - имитируется засыпка);
· моделировался выход радона из грунта в атмосферу как в варианте 1, когда в пределах грунта задан поток воздуха по проницаемым каналам с постоянной скоростью u1=const (вариант 3);
· моделировался выход радона из грунта в атмосферу как в варианте 2, когда в пределах грунта задан поток воздуха с постоянной скоростью u1=const (вариант 4).
Вариант 1.
В варианте 1 моделировался выход радона из грунта в атмосферу только за счет диффузии (u1=u2=0 ) и внутреннего источника Q=lC0, равномерно распределенного во всем слое грунта. На границе z = –z0 задано граничное условие

На границе z = z1 для моделирования свободной поверхности (ухода радона в атмосферу) величина CRn берется с предыдущего шага. При этом, в начальный момент (t=0) во всей счетной области CRn = 0. Для получения установившегося распределения радона, счет велся до выхода на стационарное решение.
Вариант 2.
В варианте 2 моделировался выход радона из грунта в атмосферу за счет диффузии, когда в грунте действовал внутренний источник радона Q=lC0, равномерно распределенный по всей глубине до 1 метра от поверхности, а на глубине от 0 до z2=1 м - грунт не выделяет радон. Граничные и начальные условия те же, что и в варианте 1.
Для удобства изображения приведем профили концентрации в относительных единицах С=CRn/C0. Пространственное распределение установившейся концентрации радона CRn(z)/C0 и временная зависимость CRn(t)/C0 в точке раздела сред (z=0) для вариантов 1,2 представлены на рис.8,9.

Рис.8. Пространственное распределение концентрации радона CRn(z)/C0 в вариантах 1,2 (z2 – толщина засыпки).
Из рис.8 видно, что во 2 варианте с метровой засыпкой выход радона из грунта в атмосферу примерно в два раза меньше чем в 1 варианте без засыпки.

Рис.9. Временная зависимость CRn(t)/C0 в точке раздела сред (z=0) в вариантах 1,2
(z2 – толщина засыпки).
Из рис.9 видно, что примерно через 40 суток на границе раздела сред устанавливается постоянное значение концентрации СRn. В первом случае СRn/C0»0.14, а во втором СRn/C0»0.06. Видно, что засыпка нейтральным грунтом сильно влияет на концентрацию радона при выходе в атмосферу.
Вариант 3.
В варианте 3 моделировался выход радона из грунта в атмосферу как в варианте 1, когда в пределах грунта задан поток воздуха по проницаемым каналам с постоянной скоростью u1=const .
В данном варианте моделировался выход радона из грунта в атмосферу, когда в грунте задавался поток воздуха, выходящий по проницаемым каналам с постоянной скоростью u1=0.001см/с и внутренний источник радона Q=lC0. В воздухе распространение радона происходит только за счет диффузии (u2=0).
Граничные и начальные условия те же, что и в варианте 1.
Вариант 4.
В варианте 4 моделировался выход радона как в варианте 3, когда на глубине от 0 до z2=1м грунт не выделяет радон.
Пространственное распределение установившейся концентрации радона CRn(z)/C0 и временная зависимость CRn(t)/C0 в точке раздела сред (z=0) для вариантов 3,4 представлены на рис.10,11.

Рис.10. Пространственное распределение концентрации радона в вариантах 3,4
(z2 – толщина засыпки).
Из рис.10 видно, что в 4 варианте с метровой засыпкой выход радона из грунта в атмосферу примерно в полтора раза меньше чем в 3 варианте без засыпки.

Рис.11. Временная зависимость концентрации радона в точке раздела сред (z=0) в вариантах 3,4 (z2 – толщина засыпки).
Из рис.11 видно, что примерно через 60 суток на границе раздела сред устанавливается постоянное значение концентрации СRn. В первом случае СRn/C0 »0.5, а во втором СRn/C0 »0.4. Видно, что моделирование конвективного переноса радона сильно влияет на концентрацию радона при выходе в атмосферу.
После описания распределения концентрации Rn, выходящего из почвы в атмосферу, были проведены расчеты для установления распределения CRn по глубине для различных значений D2.
Основные параметры задачи: коэффициент диффузии в воздухе D2=0.1 см2/с, коэффициент диффузии в грунте варьировался D1={0.1, 0.05, 0.01} см2/с, пористость грунта m=0.2, постоянная полураспада радона l=2.1×10-6 с-1, z0=9м, z1=9м. В грунте действовал внутренний источник радона Q=l, равномерно распределенный на глубине от -z0 до -1м. Моделировался выход радона только за счет диффузии, т.е. скорость конвективного переноса u1=u2=0. При этом, в начальный момент (t=0) во всей счетной области CRn = 0, на границе z = –z0 было задано граничное условие ¶CRn(z=–z0,t)/ ¶z=0, а на границе z = z1 для моделирования свободной поверхности (ухода радона в атмосферу) величина CRn бралась с предыдущего шага. Полученные зависимости CRn(z) были нормированы на экспериментальное значение CRn в точке z=0.
Данные эксперимента представлены в таблице 5
( здесь следует отметить, что ПДК по радону – 200 Бк/м3).
Таблица 5.
|
Z(cm) |
CRn (Бк/м3) |
|
0 |
970 |
|
20 |
720 |
|
50 |
380 |
|
200 |
360 |
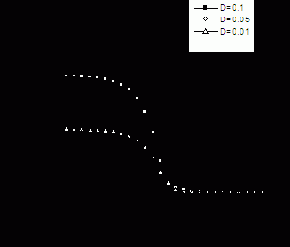
Рис.12. Распределение CRn для различных значений D1
Из рис.12 видно, что при уменьшении D1 на порядок концентрация радона в грунте уменьшается в 2 раза.
На рис.13 представлено установившееся распределение CRn по z при D1=0.1 см2/с для различных значений u1.

Рис.13. Распределение CRn для различных значений u1.
Из рис.13 видно, что при увеличении u1 на порядок концентрация радона в грунте уменьшается в 7 раз.
На рис.14 приведено сравнение установившегося распределения CRn в выделенном приповерхностном участке zÎ[0,220cm] для различных значений D1 и экспериментальных данных из таблицы 5.

Рис.14. Распределение CRn для различных значений D1.
На рис.15 представлены установившееся распределение CRn в выделенном приповерхностном участке zÎ[0,220cm] для различных значений u1 и экспериментальные данные из таблицы 5.

Рис.15. Распределение CRn для различных значений u1.
Из рисунков 14,15 видно, что в двух точках существует разница между результатами расчетов и экспериментальными данными. Разница, по-видимому, объясняется погрешностями измерений.
Рассмотрим результаты трехмерных численных расчетов по изучению радонового поля над хвостохранилищем. Цель этих расчетов состояла в определении пределов распространения вредной для здоровья концентрации радона. В этих задачах использовались экспериментальные данные измерений радиационного фона. Расчетная область совпадает с областью вокруг ХВХ, где проводились измерения гамма-фона. Первая задача - это задача на установление стационарного распределения радона над площадью хвостохранилища в безветренную погоду.Эти расчеты при отсутствии ветра позволяют оценить характерную высоту облака с его повышенным содержанием, подобрать коэффициенты модели, соответствующие изучаемому региону. Вторая задача - это исследование распределения радона над хвостохранилищем при постоянном ветре. Эти расчеты позволяют оценить количество радона, уносимого ветром с площади хвостохранилища.
